Lineaire regressie
Hoewel het principe misschien wat te eenvoudig lijkt, is good old fashioned lineaire regressie veruit het meest gebruikte model in artificiŽle intelligentie en machine learning. Lineaire regressie is als model op zich al zeer populair, maar is ook het werkpaard dat gesofisticeerde neurale netwerken tot leven brengt.
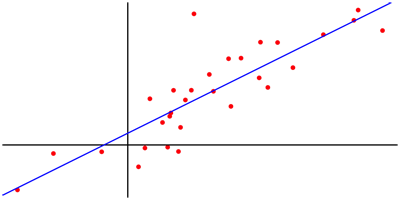
Lineaire regressie is een model waarbij men ervan uitgaat de output van een systeem evenredig evolueert met de input. In wiskundige termen wordt dat vertaald als y = a x + b, waarbij de parameters a en b zo gekozen worden dat de functie zo goed mogelijk aansluit bij de x,y-combinaties in een bepaalde dataset.
Grafisch voorgesteld komt het erop neer dat men een lijn probeert te tekenen die zo goed mogelijk aansluit bij de punten die de x,y-combinaties in de dataset voorstellen. In de wiskunde gebeurt het bepalen van de positie van die lijn heel precies, met de kleinste-kwadratenmethode. De parameters a en b worden daarbij zodanig gekozen dat de gemiddelde afstand van de punten tot de lijn zo klein mogelijk is.
Eenvoudiger kan machine learning haast niet zijn: als je van honderd mensen weet hoeveel stukken fruit ze aten per dag en hoe oud ze geworden zijn, kan je op basis van die data een functie formuleren die op basis van het aantal stukken fruit dat je eet per dag kan voorspellen hoe oud je zal worden.
Gevaar van extrapoleren
Dat voorbeeld is meteen ook goed om op een aantal risicoís te wijzen bij het toepassen van lineaire regressie. Zo zou een optimist uit de functie kunnen afleiden dat hij 120 jaar oud kan worden door elke dag 30 appels te eten, wat in realiteit niet noodzakelijk het geval is.
De verklaring hiervoor is dat het gevaarlijk is om bij lineaire regressie te extrapoleren. Als het al lukt om door de puntenwolk in een grafiek een min of meer passende lijn te trekken, zegt die lijn weinig of niets over de relatie tussen input en output buiten de range van de puntenwolk. En zelfs binnen de range moet men goed nagaan of er wel een evenredig verband bestaat tussen input en output.
Nog belangrijker is dat het model veel te eenvoudig kan zijn omdat het belangrijke invloedsfactoren (inputs) buiten beschouwing laat. In reŽle machine learning toepassingen heeft men al snel een hele reeks inputs en krijgt men dus een vergelijking als y = a1 x1 + a2 x2 + Ö + b. Maar dan nog blijft het de vraag of wel alle relevante factoren in rekening gebracht zijn.
Dat het verband tussen input en output mogelijks niet lineair is, kan opgevangen worden door meer complexe vergelijkingen te gebruiken in de regressie. Een speciaal geval hierbij is nog de logische regressie die toegepast wordt in applicaties met een binaire output. De regressie levert dan voor elke mogelijke input de verwachte binaire waarde met een waarde die de waarschijnlijkheid van die output aangeeft.
Oneindige combinatie van sommen en producten
Zoals we in de inleiding al aangaven is lineaire regressie ook het werkpaard van neurale netwerken (zie ons artikel over deep learning). Dat komt omdat er in elk neuron in zo een netwerk een gewogen gemiddelde gemaakt wordt van de inputs. Een neuron met x1, x2 en x3 als inputs zal als output dus y = a1 x1 + a2 x2 + a3 x3 + b geven, wat dezelfde vergelijking is als bij lineaire regressie. De gewichten a1, a2 en a3 worden samen met de offset b bepaald tijdens het leren, door te zoeken naar parameters die het model doen kloppen voor een set van gelabelde data, opnieuw net als bij lineaire regressie.
Het typische aan neurale netwerken is dat ze duizenden neuronen bevatten met elk hun eigen parameters zodat er geen directe wiskundige methode meer mogelijk is voor het bepalen van de parameters en het ook praktisch onmogelijk wordt om de werking van het netwerk in een wiskundige vergelijking te vatten. Maar theoretisch gezien zou het dus wel kunnen en is de vergelijking een haast oneindige combinatie van eenvoudige sommen en producten.
© Productivity.be
Feel free to share
Newsletter
News
Emersonís New Comprehensive Automation Platform Empowers Decisive Action from Plant to Enterprise
Portable authenticity testing device detects food fraud at the point of sampling
Three trends set to drive cyber-attacks in 2024
TotalEnergies Partners with Major International Companies to Support e-NG Development
Schneider Electric Collaborates with NVIDIA on Designs for AI Data Centers
Apptronik and Mercedes-Benz Enter Commercial Agreement
Agenda
15/04 - 19/04: Wire/Tube, DŁsseldorf (D)
22/04 - 26/04: Hannover Messe, Hannover (D)
14/05 - 16/05: Advanced Manufacturing, Antwerp Expo (B)
15/05 - 16/05: Advanced Engineering, Antwerp Expo (B)
15/05 - 16/05: Food Tech Event, Brabanthallen, 's-Hertogenbosch (Nl)
28/05: Industrie & Maintenance, Namur Expo (B)
05/06 - 06/06: Vision, Robotics & Motion, Brabanthallen, 's-Hertogenbosch
10/06 - 14/06: ACHEMA, Frankfurt am Main (D)
18/09 - 19/09: Kunststoffen, Brabanthallen 's-Hertogenbosch (Nl)
08/10 - 11/10: Motek, Stuttgart (D)
15/09/25 - 19/09/25: Schweissen & Schneiden, Messe Essen (D)
08/10/25 - 15/10/25: K, DŁsseldorf (D)
